
Trabalho 1 – ordenação (para 13/9)
O objetivo do trabalho é comparar alguns algoritmos de ordenação.
-
Implemente os algoritmos estudados em aula
(seleção, inserção, mergesort, quicksort, heapsort).
Escreva o programa mais simples possível para testar cada algoritmo.
Compare o esforço necessário para a implementação correta de cada algortimo.
-
Compare o desempenho dos algoritmos em
sequências de números inteiros gerados aleatoriamente.
Use sequências de 100 até 100000 números.
(E mais se for possível.)
Meça e compare os tempos de cada algoritmo.
-
Repita os testes com sequências especiais:
ordenadas em ordem crescente,
ordenadas em ordem descrescente,
com muitas repetições,
com poucas repetições.
-
No caso de mergesort e quicksort,
interrompa a recursão quando o subproblema for pequeno
e execute ordenação por inserção em cada subproblema.
No caso de quicksort,
faça o mesmo executando ordenação por inserção uma única vez,
ao final do processo.
Vale a pena fazer essas modificações?
A partir de quando?
Para qual definição de pequeno?
Trabalho 2 – grafos (para 23/10)
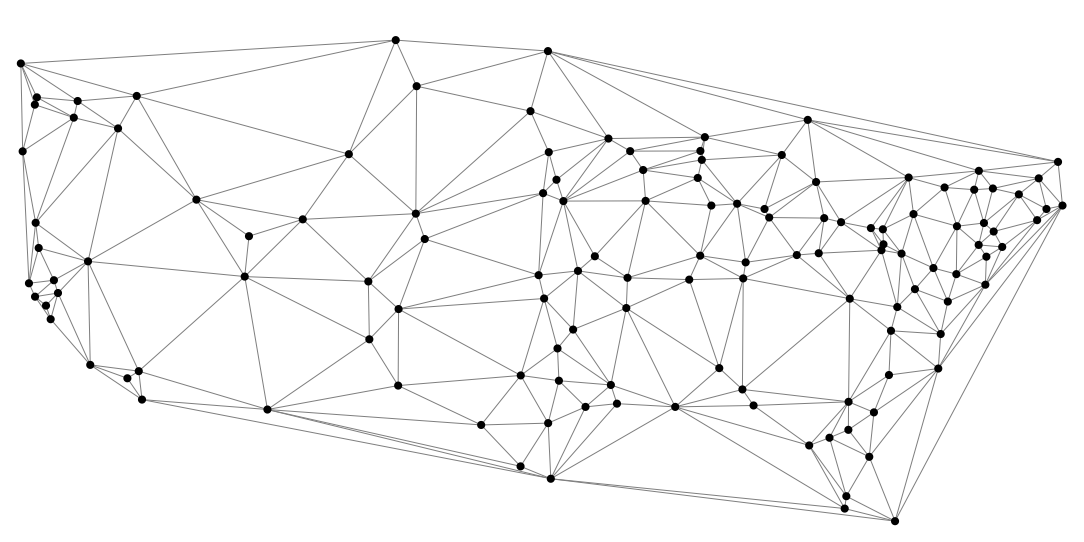 O grafo ao lado mostra 128 cidades da América do Norte.
Ele foi extraído do arquivo miles.dat do livro The Stanford GraphBase.
O arquivo map.txt representa esse grafo:
os vértices estão numerados de 1 a 128 e
cada linha lista uma aresta do grafo e o seu comprimento,
isto é,
a distância entre as cidades dadas.
O grafo ao lado mostra 128 cidades da América do Norte.
Ele foi extraído do arquivo miles.dat do livro The Stanford GraphBase.
O arquivo map.txt representa esse grafo:
os vértices estão numerados de 1 a 128 e
cada linha lista uma aresta do grafo e o seu comprimento,
isto é,
a distância entre as cidades dadas.
- Encontre uma árvore geradora mínima para esse grafo.
- Encontre o menor caminho entre a cidade 93 e a cidade 112.
- Encontre a árvore de menores caminhos a partir da cidade 104.
Para cada um desses subgrafos, calcule o comprimento total.
Se quiser gerar uma figura, edite o arquivo map.eps para incluir
o subgrafo após a linha marcada subgraph no formato indicado.
Faça o mesmo para o grafo das 5565 sedes dos municípios do Brasil,
encontrando o menor caminho entre a cidade 1 e cidade 2646,
e a árvore de menores caminhos a partir da cidade 2646.
Veja uma
imagem do grafo e o programa ps.
Trabalho 3 – fecho convexo (para 6/11)
O objetivo do trabalho é comparar algoritmos que calculam o fecho
convexo de um conjunto de pontos no plano.
-
Implemente o algoritmo de Jarvis e o algoritmo de Graham,
nas suas duas variantes.
(Implemente também outros algoritmos se quiser.)
Escreva o programa mais simples possível para cada algoritmo.
Não se preocupe com interfaces gráficas.
-
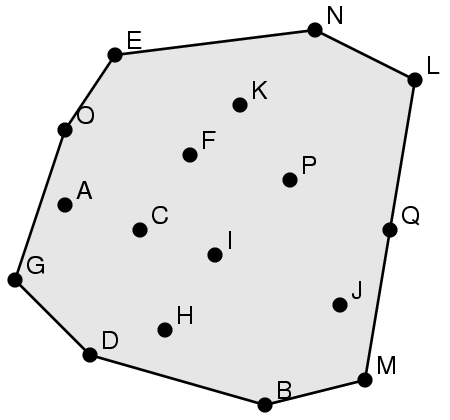 Teste os seus programas no seguinte conjunto de pontos:
Teste os seus programas no seguinte conjunto de pontos:
A B C D E F G H I J K L M N O P Q
x 3 11 6 4 5 8 1 7 9 14 10 17 15 13 3 12 16
y 9 1 8 3 15 11 6 4 7 5 13 14 2 16 12 10 8
A solução é B M L N E O G D.
Note que Q não faz parte da solução.
A
figura ao lado
mostra a solução e foi gerada por um
programa
em
PostScript.
Teste também nas 128 cidades do trabalho 2 e compare a sua solução com o mapa.
As coordenadas das cidades estão aqui.
-
Compare o desempenho dos algoritmos implementados em conjuntos de pontos
gerados aleatoriamente
dentro de um retângulo,
dentro de um triângulo,
dentro de um círculo,
e sobre o círculo.
Use conjuntos de 100 até 100000 pontos.
(E mais se for possível.)
Compare os tempos de cada algoritmo e
também o esforço necessário para sua implementação.
-
Refaça os testes do item anterior incorporando eliminação de pontos interiores.
Vale a pena eliminar pontos interiores?
-
Avalie o papel do passo de ordenação no desempenho global dos seus programas.
Qual a diferença entre usar
um algoritmo quadrático ou um algoritmo O(n log n)?
Last update:
Tue Oct 16 09:29:37 BRT 2012
. Logo borrowed from
wikipedia.



 O grafo ao lado mostra 128 cidades da América do Norte.
Ele foi extraído do arquivo miles.dat do livro The Stanford GraphBase.
O arquivo map.txt representa esse grafo:
os vértices estão numerados de 1 a 128 e
cada linha lista uma aresta do grafo e o seu comprimento,
isto é,
a distância entre as cidades dadas.
O grafo ao lado mostra 128 cidades da América do Norte.
Ele foi extraído do arquivo miles.dat do livro The Stanford GraphBase.
O arquivo map.txt representa esse grafo:
os vértices estão numerados de 1 a 128 e
cada linha lista uma aresta do grafo e o seu comprimento,
isto é,
a distância entre as cidades dadas.
 Teste os seus programas no seguinte conjunto de pontos:
Teste os seus programas no seguinte conjunto de pontos: